First published at www.reneweconomy.com.au on Aug 2 2016
The main points:
- SolarQuotes has done a great job putting together data on 28 different household storage systems on the market to date. The data shows a median capital cost of $9000 or $1800 per usable KWh (kilowatt hour), which translates to $0.39 of cost for every delivered KWh of electricity. We expect competition to really drive price. We think the installed base is less than 5000 grid connected systems, but based on Enphase orders expect that to explode to over 50,000 within the next 18 months.
- EV battery costs on the other hand are about A$250 KWh of headline capacity or say A$350 KWh of usable capacity. That is just 20% of the cost of household storage. We think inverters and the supply chain account for most of the difference. We think purpose built stationary energy lithium storage could end up cheaper than for EVs because of different chemistry, less constrained form factors, and ultimately greater scale. The question is whether EV battery costs, which themselves are falling quickly, can be pushed through to installed residential costs.
- Using EV costs on demand renewable energy wind+lithium has an LCOE of maybe A$160 MWh broadly comparable with say CST. In my view the global expansion of lithium makes it a much lower risk technology than CST, at least at this point of time. In addition there are other possibilities such as putting the storage at the fringe of the grid (behind the household meter).
- From a policy perspective it seems that some policies that incentives EVs will also progress stationary energy lithium storage. We think that would be a good thing.
Does lithium storage energy cost $50 MWh, $100MWh, or $400MWh?
Today you get one answer, but always there is someone saying that at the “end of the rainbow” there will be another answer.
In our minds we don’t really know because as yet the volumes in the market are just not high enough to give a clear road map on costs.
We estimate less than 5000 grid connected systems NEM wide
Chatting around at last week’s excellent Clean Energy Summit conference in Sydney, we tried to get a vibe of how many batteries, connected to the grid (“hybrid”) have actually been installed to date.
The answer still seems to be ‘not many.’ We think less than 5000 and would not be surprised if it was less than 2000. But we don’t know. What we do know, thanks to SolarQuotes, is that that there are lots of brands and vendors. Here at ITK we rearranged SolarQuotes data, to highlight a few points.
First we can see 28 separate vendors. For consumers, that’s great.

We calculate the median cost of a system at $9100, the median capital cost per usable KWh at $1800 and the median cost per delivered KWh of electricity at $0.39.
We think the cost is falling at about 20% per year. Some of the systems include inverters, some include installation. Not all the names are using lithium but the vast majority are.
It can be argued that simply thinking about the capital cost per KWh is too simplistic and that the cost per delivered cycle, whether warrantied or not, is a better measure. We use SolarQuotes’ calculation of warrantied cycles in Fig X. Our only caveat is that it’s easy to make your system look cheaper by promising a longer life. Time will eventually tell. In any case we show two charts – one for capital cost and one for cost (undiscounted) for delivered energy.
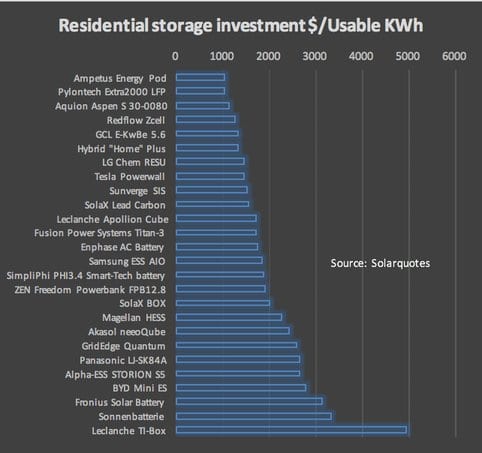
Figure 2: Capital cost per KWh of deliverable capacity
In looking at the delivered cost of energy chart what’s interesting is: (1) Tesla is now in the middle of the pack, (2) Enphase looks relatively cheap and (3) None of them is cheap enough.

Figure 3: Capital cost per KWh of lifetime energy A$ cents
Enphase appears to have been “clever” in that the absolute capital cost to be a “player” is a relatively low $2000, versus a category median of $9000, and also the cost of delivered electricity is attractive.
On that basis, it’s not surprising that advance “orders” are as much as 50000 units. Perhaps Enphase will be the Tesla of residential storage. The implication is that even if Enphase is 80% of the 2017 market then the market will grow from say 5000 units to say 60000 units.
EV battery prices imply residential costs are still 2-3X too high
We know that battery packs for EVs cost around US$200 MWh. That is the wholesale price and does not include the inverter, but it does include the BMS.
These numbers can be supported from multiple sources, of which the most detailed is from Argonne Lab BatPacC spreadsheet and documentation. Alternatively just typing “Chevvy Bolt battery cost” into Google produces in 0.73 seconds of research:
“Electric-car battery costs: Tesla $190 per kwh for pack, GM $145 for cells. Lithium-ion cells and the battery packs that hold them are the single most costly part of modern electric cars.” Source: Google search July 2016
To our way of thinking if there was enough volume, stationary energy storage using LiFe4 would be cheaper than automotive storage which mainly uses some variant of LiNiCo.
The Chevvy Bolt battery will be warrantied for 10 years or 100,000 miles. This is roughly about 3500 cycles. However, the expectation in the industry is that the battery will still have a lot of life in it, maybe not enough to provide the same power and range than an EV requires. In a household (stationary energy) context it would likely have more life. The number of cycles has a major impact on the economics of such a battery used for stationary energy.
At EV battery prices “on demand” renewable energy LCOE is $160 MWh
We assume a low 6% WACC for our calculations. Actually at 6% its likely the LCOE of wind is less than $85 MWh but no matter. The LCOE of storage is around $80-$105 MWh depending on the assumption of the number of cycles, ignoring tax and ignoring maintenance costs. So it’s definitely a best case number. We also ignore round trip energy losses. The basic motivation for the calculation was as a comparison with CSP.
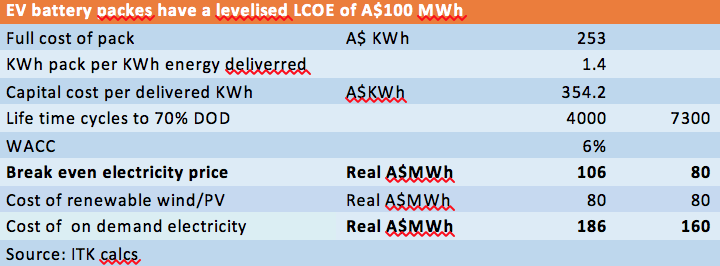
Figure 4: LCOE of storage and “on demand” renewables using EV battery costs
Although the combined wind/lithium, PV/lithium is over A$160 MWh it works from an assumption that all of the renewable energy needs to be stored and then released. It may be that only some fraction of storage is required.
Secondly it works from the assumption that all the energy is being produced and stored on a utility scale with the associated transmission and distribution infrastructure. If we get down to the micro grid (and the household is the ultimate micro grid), then the grid infrastructure costs become relevant.
David Leitch is principal of ITK. He was formerly a Utility Analyst for leading investment banks over the past 30 years. The views expressed are his own. Please note our new section, Energy Markets, which will include analysis from Leitch on the energy markets and broader energy issues. And also note our live generation widget, and the APVI solar contribution.
